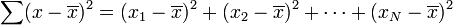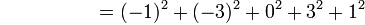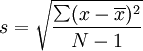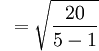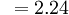2. You can multiply (or divide) both sides of an inequality by the same positive number.
3. You can multiply (or divide) both sides of an inequality by the same negative number if you reverse the inequality sign.
**You flip the sign of the inequality when you multiply or divide by a negative number.
3x-9 is greater than or equal to 9 3x-9 is less than or equal to -9
3x greater or equal 18 3x less or equal 0
x greater or equal 6 x less or equal 0
8x+6>30
subtract 6 from both sides
8x>24
divide both sides by 8
x>3
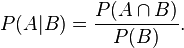

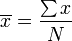
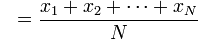
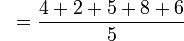
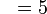
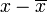 for each value in the sample:
for each value in the sample: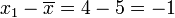
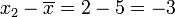
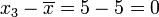
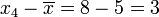
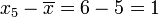
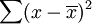 :
: