11-1

11-1 Polar and Rectangular

Rectangular Form is stated as (x,y)
Polar Form is stated as (r,y)

To convert from polar to rectangular use the formulas:
~y=rsiny
~x=rcosy

To convert from rectangular to polar use the formulas:
~r=sqrt. x^+y^2
~y=tan^-1(y/x)
________________________________________________________

Ex.1: Give the rectangular coordinates for (4,60)
You plug these numbers into the formula
y=4sin60
x=4cos60
Usually you use the trig chart to figure these out,or you can use your calculator
y=4(.5)
x=4(.866)
~Multiply the equations.
y=2
x=3.464
~Put in point form.
(3.464,2)

Ex.2: Find the polar coordinates of (5,6)
Plug numbers into the formula
r= the square root of x^2 + y^2
r= the square root of 5^2 + 6^2 =7.810

y=tan^-1(6/5)
~Solve the two equations.
r=8
y=50.194
~Put into two points.
(8,50.194)
(-8,50.194)

Plane Curves

Plane Curves... yeah.

So the different types of curves we need to know are:

1. Lemniscate
2. Cardioid
3. Rose
4. Limascon of Pascal
5. Spiral of Archimedes

For the test, you will need to know what each one looks like, and how the equation of each one looks like.

A Lemniscate looks like:
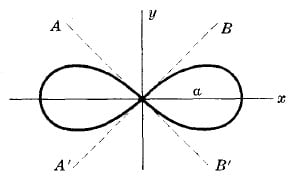and it's equation will either look like...

1. r² = a²cos2Θ
2. r = ± √(a²cos2Θ)
Ex. r² = 9cos2Θ
r = ± √(9cos2Θ)

A Cardioid resembles..a heart..kinda.
It's equation will look like ---> r = a + acosΘ.
Ex. r = 3 + 3cosΘ
r = 5 + 5cosΘ

A rose will obviously look like a flower of sorts.
The equation will look like: r = asinbΘ or r = acosbΘ

To find the number of petals, if b is odd, it has b petals. If b is even, it has 2b petals.

Ex. 3sin8Θ has 16 petals

3cos9Θ has 9 petals

A Limascon of Pascal looks similar to a Cardioid:
the equations looks like: r = b + acosΘ
the difference between a Cardioid and a Limascon is that b is not equal to a.

To find if it has an inner loop or not, if a is greater than b, it does, if a is less than b, it does not.

Ex. 3 + 5cosΘ does have an inner loop

5 + 3 cosΘ does not have an inner loop


A Spiral of Archimedes is a spiral, obviously :P
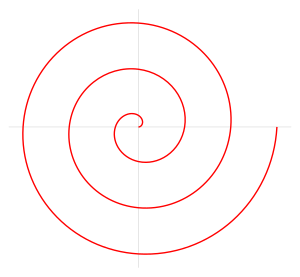LOOK HOW PRETTY!! Haha, uh, the equation is pretty much r = aΘ

Ex. r = 8Θ

Complex numbers

Complex numbers in rectangular form: z=x+yi

Complex numbers in polar form: z=rcos(theta)+rsin(theta)i

i=square root of -1 and cannot be simplified and e^ipi=-1

absolute value of z=square root of x^2+y^2

To multiply complex numbers:

1. Rectangular-FOIL i^2=-1

2. Polar-multiply r and add theta

Example 1:

Express each complex number in polar form. Give angle measures to the nearest degree when necessary.

1+isquare root of 3

r=square root of1^2+isquare root of 3^2

r=square root of 1+3

r=square root of 4

r=+/-2

theta=tan^-1(square root of 3/1)=60degrees

theta=60degrees and 240degrees

z=2cis60degrees

z=2cis240degrees

z=+/-2cos240degrees+2sin240degrees

Example 2:

Express each complex number in rectangular form.

(5cis30degrees)(2cis60degrees)

5(2)=10

60+30=90

10cis90degrees

x=10cos90degrees

y=10sin90degrees

x=0

y=10

0+10i=10i

11-4

Easiest lesson..longest problems..

Formula: n square root of z= z^1/n cis (theta/n + k times 360/n)
k= 1, 1, 2, , n-1

Example 1: The cube root of 8i
0+8i
r= square root of 0^2+8^2
= plus of minus square root of 8

theta= tan inverse 8/0 = undefined
= 90 and 270

3 square root of z= 8cis90
z1/3=8 1/3cis(90/3 + 0 times 360/3)
z1/3=8 1/3cis(90/3+ 1 times 360/3)
z1/3=8 1/3cis(90/3+ 2 times 360/3)

z1/3=2cis(30)
z1/3=2cis(150)
z1/3=2cis(270)

Hope everyone had a great holiday! Kayla :)

11-1!

~Rectangular Form is stated as (x,y)

~Polar Form is stated as (r,y)

To convert from polar to rectangular use the formulas:

~y=rsiny

~x=rcosy

To convert from rectangular to polar use the formulas:

~r=sqrt. x^+y^2

~y=tan^-1(y/x)

________________________________________________________

Ex.1: Give the rectangular coordinates for (3,30)

~First plug the point into the formulas.

y=3sin30

x=3cos30

~Now either use the trig chart or the unit circle to solve these equations.

y=3(1/2)

x=3(sqrt3/2)

~Multiply the equations.

y=1.5

x=3sqrt3/2

~Put in point form.

(3sqrt3/2,1.5)

Ex.2: Find the polar coordinates of (3,4)

~First plug into the formulas.

r=sqrt3^2+4^2

y=tan^-1(4/3)

~Solve the two equations.

r=5

y=53.13,126.87

~Put into two points.

(5,53.13)

(-5,126.87)

Geometric Representation of Complex Numbers

I almost forgot to do my blog tonight, but my bestttfriennddd Danielle reminded me :-)

*Complex numbers are in the form of z=x+yi in rectangular form.
*Complex numbers are in the form of z=rcos(theta)+rsin(theta)i in polar form.
**Remember that i=square root of -1 and cannot be simplified.

***e^ipi=-1

*absolute value of z=square root of x^2+y^2

*To multiply complex numbers:
1. Rectangular-FOIL *i^2=-1
2. Polar-multiply r and add theta

Example 1:
Express each complex number in polar form. Give angle measures to the nearest degree when necessary.
-1+i
r=square root of -1^2+i^2
r=square root of 1+1(i^2=1)
r=+/-square root of 2
theta=tan^-1(square root of -1/-1)=1=45degrees
theta=135degrees and 315degrees
z=+/-square root of 2cis135degrees
z=+/-square root of 2cis315degrees
z=+/-square root of 2cos315degrees+square root of 2sin315degrees

Example 2:
Express each complex number in polar form. Give angle measures to the nearest degree when necessary.
1+isquare root of 3
r=square root of1^2+isquare root of 3^2
r=square root of 1+3
r=square root of 4
r=+/-2
theta=tan^-1(square root of 3/1)=60degrees
theta=60degrees and 240degrees
z=2cis60degrees
z=2cis240degrees
z=+/-2cos240degrees+2sin240degrees

Example 3:
Express each complex number in rectangular form.
(5cis30degrees)(2cis60degrees)
5(2)=10
60+30=90
10cis90degrees
x=10cos90degrees
y=10sin90degrees
x=0
y=10
0+10i=10i

11-2

Hope everyone had a good Thanksgiving holiday :)
So the week before the holidays we learned polar and rectangular:

-Complex numbers are in the form of z=x+y; h rectangular
-In polar complex numbers are in the form of z=rcos(theta)+rsin(theta)
-This is abbrevated as z=rcis(theta)
-Absolute value of z=square root of x^2+y^2
-To multiply complex numbers
1. Rectangular, FOIL *i^2= -1
2. Polar, multiply r and add theta

Example 1:
-1+i
r= square root of (-1)^2 + i^2
= square root of 1+1
= + or - square root of 2

theta= tan inverse of 1 is square root of -1 over -1 = tan 45
negative in the second and fourth: 135 and 315
z= square root of 2cis135

Example 2:
6cis100
y=6sin100 x=6cos100
y=5.909 x=-1.042
z=-1.042+5.909i

--Danielle :)

Half Angle Formulas

Half Angle Formulas

Cos x/2 = +/- √((1+cosx)/2)                          Sin x/2=+/-√((1-cos x)/2)

1.       Find the exact value of 3π/8

The first thing you do is figure out the quadrant that 3π/8 is in.  That quadrant is the first quadrant because it is 67.5˚.  So we know that cos is positive in quadrant I. 

3π/8=(1/2)(3π/4)

Using the half angle formula with x=3π/4

Cos  3π/8=+√(1+cos(3π/4)/2)

 =+√((1-√2/2)/2)

=√(2-√2)/2

2.       Simplify  √[1-cos 80˚)/2}\]

First you have to recognize this as the half angle formula for sin because of the negative in the square root.

So you half that angle and get 40˚

So the answer is sin 40˚.

Jenna Roussel

Double Angle Formulas

Double Angle Formulas

Cos 2α=cos²α-sin²α                                Sin 2α = 2 sinα cosα

1.       Simplify  2 sin 10˚ cos 10˚

First you have to recognize this as the double angle formula for sin.

Then you multiply the given angle by 2.  So 10 times 2 is 20

The final simplified answer is sin 20˚

2.       Simplify  cos²15˚ - sin²15˚

First you recognize this as the double angle formula for cos

Then you multiply the given angle by 2.  So 15 times 2 is 30

That gives you cos 30˚=√3/2

3.       Find sin 2A and cos 2A if sin A= 5/13.

First you find cos A.  y=5, r=13, using Pythagorean thm you get that x=12.  So that means that cosA = 12/13

a.       Sin 2A = 2sinAcosA

=2(5/13)(12/13)

=120/169

b.      Cos 2A = cos²A-sin²A

=(12/13)²-(5/13)²

= (144/169) – (25/169)

= 119/169

Jenna Roussel

11-2

1+i square root of 3

r=square root of 162+square root of 3^2                                  theta=tan^-1(square root of 3)
r=square root of 4                                                                     theta=60 degrees, and 240 degrees
r=+/-2

First you use the formula r= square root of x^2 +y^2.  When you solve that, you get the square root of 4.  The square root of 4 equals plus or minus 2.  Once you solved that, you use the other formula.  The other formula is theta equals tan of negative 1 of y/x.  Now you have tan^-1(square root of 3/1).  That is tan^-1(square root of 3).  From the trig chart, we know that tan of square root of 3 equals 60 degrees.  Now you use the unit circle to find the other angle.  Tan is positive in quadrant three as well as quadrant one.  So now you add 180 to 60 and you get 240 degrees.  So 60 degrees and 240 degrees are your two answers.

Solving For Theta

To solve for theta (@) the steps are different than an algebra equation.
1.Isolate the trig function
2.Take inverse of the trig function.
such as sin-1 cos-1
arc sin arc cos
3.Use trig char or calculator to find value. Only use the value after three decimal places if got more.
4.Use the four quadrants to find the right angle + # or -# with trig function. There are always atleast two answers for each inverse. You get one and find the other.
*To move in quadrants: Q1 to Q2 = make -# and add 180
Q1 to Q3 = add 180
Q1 to Q4 = make -# add 360

EX1 cos -1 (square root 2/2)
1.From trig chart cos = 45
2. Since its positive fin other positive answer. Move to quadrant 4
-45+360=315
3. Your two answers are (45,315)

Polar Cordinates

In class we learned about polar and rectangular coordinates. 
 
(raduis, theta) is the same as (x,y) when using polar graphs. 


To convert from polar to rectangular you use:
x=rcostheta
y=rsintheta


To convert form rectangular to polar you use: 
r=square root of x^2+y^2
theta=tan^-1 (y/x)

Both of these are on the unit circle.


Example 1


What is (12,5) in polar coordinates?
r^2=√12^2+5^2
r^2=√144+25
r^2=√169
r^2=13


tan(theta)=(5/12)
theta=tan^-1(5/12)
theta=22.6 

11-1

This week in class we learned about polar coordinates and rectangular.

When using polar graphs using angles you use(radius,theta) instead of rectangular which is (x,y). To convert from polar to rectangularx=rcostheta y=rsintheta which is on the unit circle
To convert from rectangular to polar r=square root of x^2+y^2 theta=tan^-1(y/x) which is also on the unit circle!

Example 1.)
Give the rectangular coordinates for (3, 60 degrees)
y=3sin60 x=3cos60
y=3(square root of 3 over 3) x=3(1/2)
y=square root of 3 x=3/2
so the answer is (3/2, square root of 3)

Example 2.)
Give the polar coordinates for (4,4)
r= square root of 4^2+4^2 theta=tan inverse of (4/4)
r=+or-square root of 32 theta=45 degrees, 225 degrees
so the answer is (+square root of 32, 45 degrees) and (-square root of 32, 225 degrees)

11-1 Polar

This week we learned polar.

When using polar graphs using angles(r,theta) instead of (x,y)

To convert from polar to rectangular
x=rcostheta y=rsintheta
**Unit circle

To convert from rectangular to polar
r=square root of x^2+y^2 theta=tan^-1(y/x)

**Unit circle

Example 1: Give the rectangular coordinates for each point.

b.(-3,90degrees)
x=rcostheta y=rsintheta
x=-3cos90degrees
x=-3(0)
x=0
y=-3sin90degrees
y=-3(1)
y=-3
(0,-3)

c.(1,5pi/6)
x=rcostheta y=rsintheta
x=1cos30degrees
x=1(square root of 3/2)
x=square root of 3/2
y=1sin30degrees
y=1sin(1/2)
y=1/2
(-square root of 3/2,1/2)

d.(2,3pi/4)
x=rcostheta y=rsintheta
x=2cos(3pi/4)
x=2cos(square root of 2/2)
x=2(square root of 2/2)
x=square root of 2
y=2sin45degrees
y=2sin(square root 2/2)
y=square root of 2
(-square root of 2,square root of 2)

--Danielle

11-1

(-2,2)

r=square root of -2^2+2^2=square root of 8
 theta=tan^-1(-2/2)
theta=45 degrees
(square root of 8, 45 degrees)
(-square root of 8,135 degrees)

To get (-2,2) in polar coordinates, you have to use the formula r=square root of x^2+y^2.  So plug your coordinate you are given into the formula and you get the square root of 8.  Then you have to use the other formula which is theta=tan^-1(y/x).  You have to plug in the points you are given into this formula and you get 45 degrees and 135 degrees from the trig chart and unit circle.  Now all you have to do is plug your answers into the coordinates.  So now you have that your polar points are (square root of 8, 45 degrees) and (-square root of 8, 135 degrees).

Polar!

I hope everyone has a great week and a Happy Thanksgivingg! :-)

Graphs using angles(r,theta) instead of (x,y)

To convert from polar to rectangular *unit circle*
x=rcostheta y=rsintheta

To convert from rectangular to polar *unit circle*
r=square root of x^2+y^2 theta=tan^-1(y/x)

Example 1:
Give polar coordinates (r,theta), where theta is in degrees, for each point.
a. (-2,2)
r=square root of 2^2+2^2
r=square root of 8
r=+/-2square root of 2
theta=tan^-1(2/-2)
theta=tan^-1(-1)
theta=135degrees and 315degrees
(2square root of 2,135degrees)
(-2square root of 2, 315degrees)

b.(5,0)
r=square root of 5^2+0^2
r=square root of 25
r=+/-5
theta=tan^-1(0/5)
theta=tan^-1(0)
theta=0degrees, 180degrees, 360degrees
(5,0)

c.(square root of 2,-square root of 2)
r=square root of the square root of 2^2+-square root of 2^2
r=square root of 2+2
r=square root of 4
r=+/-2
theta=tan^-1(-square root of 2/square root of 2)
theta=tan^-1(-1)
(2,-45)

d.(-square root of 3,1)
r=square root of the -square root of 3^2+1^2
r=square root of 3+1
r=square root of 4
r=+/-2
theta=tan^-1(1/-square root of 3)
theta=tan^-1(-square root of 3/3)
theta=150degrees and 315degrees
(2,150degrees)
(-2,315degrees)

Example 2:
Give the rectangular coordinates for each point.
a.(4,120degrees)
x=rcostheta y=rsintheta
x=4cos120degrees
x=4(1/2)
x=2
y=4sin120degrees
y=4(square root of 3/2)
y=4square root of 3/2
y=2square root of 3
(-2,2square root of 3)

b.(-3,90degrees)
x=rcostheta y=rsintheta
x=-3cos90degrees
x=-3(0)
x=0
y=-3sin90degrees
y=-3(1)
y=-3
(0,-3)

c.(1,5pi/6)
x=rcostheta y=rsintheta
x=1cos30degrees
x=1(square root of 3/2)
x=square root of 3/2
y=1sin30degrees
y=1sin(1/2)
y=1/2
(-square root of 3/2,1/2)

d.(2,3pi/4)
x=rcostheta y=rsintheta
x=2cos(3pi/4)
x=2cos(square root of 2/2)
x=2(square root of 2/2)
x=square root of 2
y=2sin45degrees
y=2sin(square root 2/2)
y=square root of 2
(-square root of 2,square root of 2)

Polar and Rectangular!

~Rectangular Form is stated as (x,y)

~Polar Form is stated as (r,y)

To convert from polar to rectangular use the formulas:

~y=rsiny

~x=rcosy

To convert from rectangular to polar use the formulas:

~r=sqrt. x^+y^2

~y=tan^-1(y/x)

____________________________________________________________

Ex.1: Give the rectangular coordinates for (2,30)

~First plug this point into the formulas

x=2cos30

y=2sin30

~Now use either your trig chart or your calculator to solve the equation.

x=2(sqrt. 3/2)

y=2(1/2)

~Multiply out the answers

x=2sqrt.3/2

y=1

~Put your answer in point form.

(2sqrt3/2,1)

Ex.2: Give the polar coordinates for the point (2,-2)

~First plug this point into the formulas

r=sqrt. 2^2+(-2)^2

y=tan^-1(-2/2)

~Now solve the two equations.

r=+/- sqrt8

y=135, 315

~Finally put the answers into two points.

(-sqrt8, 315)

(sqrt8, 135)

~

polar and retangular

Rectangular is the form (x,y), which is our normal form. This is used for lines and quadrants. There is another way graph using polar. Polar graphing is used with circlular graphs. There are ways to convert between these two forms. The form for polar is (#,#degrees). The form for rectangular is (x,y) ofcourse.

*to graph a polar graph you must use angles (r,@) instead of (x,y). To graph in calculator you must go to mode and switch to radians and polar.

-To convert from polar to rectangular x=rcos@ y=rsin@
-To convert from rectangular to polar r=squareroot of x^2+y^2 and @=tan-1(x/r)

Ex1. Convert (8,60degrees) to rectangular
X=8cos(60) Y=8sin(60)
8(1/2) 8(squareroot 3/2)
(8/2) 8squareroot3/2

Ex2 convert (1,1) to polar
r=squareroot 1^2+1^2 Tan-1(1)
r=+-2 Tan =45 and 225

(2,45)
(-2,225) same point

Polar

Use (r, θ) instead of (x, y) to graph

To convert from polar to rectangular x = rcosθ y = rsinθ

To convert from rectangular to polar r = sqrtx^2+y^2 θ = tan^-1(y/x)

Ex 1. Give the polar coordinates for the point (3,4)

r = sqrt3^2 + 4^2 θ = tan^-1(4/3)

r = sqrt25 = +/-5 θ = 53.130° add 180° for the second point – 233.130°

(5, 53°7’48”) and (-5, 233°7’48”)

Ex 2. Give the rectangular coordinates for (3, 30°)

x = 3cos30° y = 3sin30°

x = 3(sqrt3/2) y = 3(1/2)

x = 3sqrt3/2 y = 3/2

(3sqrt3/2, 3/2)

Polar and Rectangular

Instead of using (x,y), you use (r, θ).

To convert from polar to rectangular, use the following formulas: 

x=rcosθ

y=rsinθ

To convert from rectangular to polar, use the following formulas:

r=√x^2+y^2

θ=tan^-1(y/x)

Give the polar coordinates for the point (0,5)

r=√0^2+5^2

 =√25

 =5

θ=tan^-1(5/0)

  =undefined

Polar and Rectangular

Graph using (r, θ) instead of (x, y)

To convert from polar to rectangles x = rcosθ y = rsinθ

To convert from rectangles to polar r = sqrtx^2+y^2 θ = tan^-1(y/x)

Ex 1. Give the polar coordinates for the point (3,4)

r = sqrt3^2 + 4^2 θ = tan^-1(4/3)

r = sqrt25 = +/-5 θ = 53.130° add 180° for the second point – 233.130°

(5, 53°7’48”) and (-5, 233°7’48”)

Ex 2. Give the rectangular coordinates for (3, 30°)

x = 3cos30° y = 3sin30°

x = 3(sqrt3/2) y = 3(1/2)

x = 3sqrt3/2 y = 3/2

(3sqrt3/2, 3/2)

double angle

It's sort of late,but i still managed to remember to do this ;)

The lesson learned this week included 10 new formulas in order to solve these problems. You could memorize them to study or use cards.

Here are all of the formulas used to solve these problems:

1. sin2alpha= 2sinalphacosalpha

2. cos2alpha= cos^2A-sin^2A

3. sin2alpha= 1-2sin^2A

4. sin2alpha= 2cos^2alpha-1

5. tan2alpha= 2tanalpha/1-tan^2alpha

6. sin alpha/2= +/- square root of 1-cosalpha/2

7. cos alpha/2= +/- square root of 1+ cosalpha/2

8. tan alpha/2= +/- square root of 1-cosalpha/1+cosalpha

9. square root of 1-cosalpha/1+cosalpha= sinalpha/1+cosalpha

10. sinalpha/1+cosalpha= 1-cosalpha/sinalpha

Example problem

1. 2sin(45)cos)

sin2(45)=sin(90)

You are just simplifying this problem.

1-cos(10)/ sin(10)

tan(10)/2=tan(5)

For this problem cos and sin turn into tan.

Simplify:

2cos^2(20)-1

cos2(20)= cos40

=4 square root of 5

LOOVEYALL:)

So check me out i just got off a 3 hour practice right, and i just remembered to do this blog lol

Only thing i know how to do is the tan formulas hah

i know tan(x+Y)= tan x + tan y/ 1-tanx * tany
problem: tan x = 3/4 and tan y = 5/8. Find tan(x+y)
=(3/4) + (5/8)/ 1- (3/4)(5/8)
=11/8/ 1-(15/32)
=11/8 / 17/32
=44/17

Yea thats a blog big Dooley Style ya digg
Im going to bed now im out... peace

10-3

Lesson 10-3 was about using Double Angle/Half Angle formulas. This lesson included 10 new formulas that needed to be learned in order to solve these problems. You could easily write down the formulas on note cards to study or if you're like me and learn by doing things, then you can just keep doing example problems until you remember the formulas.

The formulas included:

1. sin2alpha= 2sinalphacosalpha

2. cos2alpha= cos^2A-sin^2A

3. sin2alpha= 1-2sin^2A

4. sin2alpha= 2cos^2alpha-1

5. tan2alpha= 2tanalpha/1-tan^2alpha

6. sin alpha/2= +/- square root of 1-cosalpha/2

7. cos alpha/2= +/- square root of 1+ cosalpha/2

8. tan alpha/2= +/- square root of 1-cosalpha/1+cosalpha

9. square root of 1-cosalpha/1+cosalpha= sinalpha/1+cosalpha

10. sinalpha/1+cosalpha= 1-cosalpha/sinalpha

Example problem using a formula:

1. 2cos^2 10 degrees-1

-This example problem represents the formula sin2alpha= 2cos^2alpha-1

-Becomes cos2(10) which equals cos20degrees

Example problem number 2 using a formula:

2. 2 sin alpha/2 cos alpha/2

-This example problem represents the formula sin2alpha= 2sinalphacosalpha

-Becomes sin2 (alpha/2); the 2's cancel out and you're left with sinalpha.

10-2

tan theta=1/4
tan theta=3/5
tan(theta+beta)=tan(1/4+3/5)=tan theta+tan beta/1-tan theta*tan beta
(1/4)+(3/5)/1-(1/4)*(3/5)=5/20+12/20/1-3/20=17/20/17/20=1

In this problem, you are given tan theta and tan beta.  First to solve this problem, you need to know the formula.  The formula that you need is tan theta+tan beta/1-tan theta*tan beta.  Now that you have the formula, you just plug in the numbers you are given into the formula.  So now you have 1/4+3/5/1-1/4*3/5.  First in solving this equation, you have to find common denominators so you can add the top two fractions.  20 is the common denominator I used, so I had 5/20+12/20.  That gave me 17/20.  Next for the bottom half of the equation, you multiply the two fractions first and get 1-3/20.  Then you subtract 1 form 3/20 and get 17/20.  Now you have 17/20/17/20.  That equals 1.

Solving Trig Equations

When solving a trig equation, these guidelines may be helpful:
*you may want to sketch a quick graph to see what the solutions are
*transform the functions of 2x into functions of x by using identities, if the equation involves functions of 2x and x
*if the equation involves functions of only 2x, you would probably want to solve for 2x first and then x afterwards
*make sure you don't lose roots when dividing both sides by a function of a variable

Example 1:
sec^2theta=9
square root both sides
sec(theta)=+/-3degrees
theta=sec^-1(3)
theta=cos^-1(1/3)
=70.529
you have to take the value of all four quadrants because you get a positive and negative number when you square root
theta=70degrees31'44''
109degrees28'15''
250degrees31'44''
289degrees28'15''

Example 2:
tan^2theta=1
square root both sides
tan(theta)=+/-1
theta=tan^-1(1)
tan is positive and negative in all four quadrants
theta=45degrees
135degrees
225degrees
315degrees

Example 3:
1-csc^2(theta)=-3
subtract 1 from both sides
-csc^2(theta)=-4
divide both side by -1
csc^2(theta)=4
square root both sides
csc(theta)=+/-2
theta=csc^-1(2)
sin is positive and negative in all four quadrants
theta=30degrees
150degrees
210degrees
330degrees

Example 4:
8cos^2(theta)-3=1
add 3 to both sides
8cos^2(theta)=4
divide both sides by 8
cos^2(theta)=1/2
square root both sides
theta=cos^-1(square root of 2/2
theta=45degrees
135degrees
225degrees
315degrees

Example 5:
6sin^2(theta)-7sin(theta)+2=0
factor
(6sin^2-4sin)-(3sin+2)=0
group and factor again
2sin(3sin-2)-1(3sin-2)=0
set both equal to 0
2sinx-1=0 & 3sinx-2=0
sinx=1/2 sinx=2/3
x=sin^-1(1/2) x=sin^-1(2/3)
sine is positive in the first and second quadrants
x=30degrees,150degrees x=41.810degrees,138.19degrees
x=30degrees,41degrees48'36'',138degrees11'24'',150degrees

10-2

10-2

Formulas:

1) tan(a+b) = tan(a)+tan(b)/1-tan(a)tan(b)

2) tan(a-b) = tan(a)-tan(b)/1+tan(a)tan(b)

Example 1: tan alpha= 2 tan beta= -1/3

First we need to see what formula we’re going to use, the first one tan(a+b). Now you plug into the formula.

2+(-1/3) over 1-(2)(-1/3) = 5/3+(-2/6) over 1-(-2/3) =(4/3) over (5/3), you’re going to sandwich, = 12/13 = 4/5 finally answer J

Example 2: tan75º-tan30º/1+tan75ºtan30º

You’re going to use formula two. tan(a-b)

tan(75º-30º)= tan45º= 1

Example 3: tan100º+tan50º/1-tan100ºtan50º

You’re going to use the first formula.

tan(100º+50º)=tan150, find a reference angle, -tan30º= negative square root of 3 over 3

Example 4: tan alpha= 2/3 tan beta= ½

First you need to figure out what formula you need to use, the first one. tan(a+b). Plug into the formula.

2/3+1/2 over 1-(2/3)(1/2) = 4/6+3/6 over 1-(2/6)= 7/6 over 4/6, sandwich, 42/24 = 7/4 finally answer J

--Danielllllle

Double Angle Formulas

The double angle formulas are used just like the other trigonomic formulas. You must first identify it as a double angle which is really easy. One way is that there will me the function 2 then theta (@). Most of the time however you will be asked to simplify it. Then you will just take the information and plug it into the other half of the formula.

sin2@=2sin@cos@

cos2@=cos^2@-sin^2

cos2@=1-2sin^2

cos2@=2cos^2@-1

tan2@=2tan@/1-tan^2@

Ex1. Simplify cos^2(30)-sin^2(30)
A.First idenitify formula. cos2@=cos^2@-sin^2@
B.Then plug in. cos2(30)
C.Then solve. cos60=squareroot of 3/2 (From trig chart)
Done!!!

10-2

Formulas:

1) tan(a+b) = tan(a)+tan(b)/1-tan(a)tan(b)

2) tan(a-b) = tan(a)-tan(b)/1+tan(a)tan(b)

Ex. 1.) Find tan (a + b) If a is 2/3 and b is 1/2.

-You would use the first formula, tan(a)+tan(b)/1-tan(a)tan(b).

-It would be 2/3 + 1/2/1-2/3(1/2).

-You have to get a common denominator for the top and bottom, so

it would then become 2/2 (2/3) + 1/2 (3/3)/1-2/2 (2/3)(1/2) 3/3

-It would then become 4/6 + 3/6/ 4/6, making it 7/6/4/6, which equals 42/21.

you have to get the numbers to have a common deno so you can solve it, so you have to multiply the 3 by 2 and the 2 by 3. you will get 4/6 and 3/6. Then you have to multiply the bottom numbers so its 1-2/6= 6/6-2/6= 4/6. 1 is the same as 6/6, so it's 6/6-2/6=4/6.

Then its 7/6/4/6. so then you sandwich it. 7 times 6 and 6 times 4. so it's 42/21. then you have to simplify it. so the answer is 2.

Double-Angle And Half-Angle Formulas

This week we learned about Double- Angle and Half-Angle formulas. 

Double-Angle Formulas:

sin2(alpha)=2sin(alpha)cos(alpha)

cos2(alpha)=cos^2(alpha)-sin^2(alpha)

cos2(alpha)=1-sin^2(alpha)

cos2(alpha)=2cos^2(alpha)-1

tan2(alpha)=2tan(alpha)/1-tan^2(alpha)

Half-Angle Formulas:

sin(alpha)/2=+/-square root of 1-cos(alpha)/2

cos(alpha)/2=+/- square root of 1+cos(alpha)/2

tan(alpha)/2=+/- square root of 1-cos(alpha)/1+cos(alpha)

tan(alpha)/2=sin(alpha)/ 1+cos(alpha)

tan(alpha)/2=1-cos(alpha)/ sin(alpha)

Steps: 

1- Figure out which formulas going to be used

2- Fill in the formula

3- Simplify

4- Work

10-2

We've recently learned 10-2. This lesson reflected off of lesson 10-1 so it was basically the same method. 2 new formulas were learned. In these formula's the top sign is the same as what you are doing and the bottom is the opposite of what you're doing.

Formulas:

1) tan(a+b) = tan(a)+tan(b)/1-tan(a)tan(b)

2) tan(a-b) = tan(a)-tan(b)/1+tan(a)tan(b)

Ex. 1.) Find tan (a + b) If a is 2/3 and b is 1/2.
-You would use the first formula, tan(a)+tan(b)/1-tan(a)tan(b).

-It would be 2/3 + 1/2/1-2/3(1/2).

-You have to get a common denominator for the top and bottom, so

it would then become 2/2 (2/3) + 1/2 (3/3)/1-2/2 (2/3)(1/2) 3/3

-It would then become 4/6 + 3/6/ 4/6, making it 7/6/4/6, which equals 42/21.

you have to get the numbers to have a common deno so you can solve it, so you have to multiply the 3 by 2 and the 2 by 3. you will get 4/6 and 3/6. Then you have to multiply the bottom numbers so its 1-2/6= 6/6-2/6= 4/6. 1 is the same as 6/6, so it's 6/6-2/6=4/6.
Then its 7/6/4/6. so then you sandwich it. 7 times 6 and 6 times 4. so it's 42/21. then you have to simplify it. so the answer is 2.

Double Angle

This past week in class we learned how to do the double- angle formula. I find this hard so I got my sister to help me with the homework and I am finally getting the hang of it. :)

Here are the Formulas we used in class:

Double-Angle Formulas:

sin2(alpha)=2sin(alpha)cos(alpha)

cos2(alpha)=cos^2(alpha)-sin^2(alpha)

cos2(alpha)=1-sin^2(alpha)

cos2(alpha)=2cos^2(alpha)-1

tan2(alpha)=2tan(alpha)/1-tan^2(alpha)

Half-Angle Formulas:

sin(alpha)/2=+/-square root of 1-cos(alpha)/2

cos(alpha)/2=+/- square root of 1+cos(alpha)/2

tan(alpha)/2=+/- square root of 1-cos(alpha)/1+cos(alpha)

tan(alpha)/2=sin(alpha)/ 1+cos(alpha)

tan(alpha)/2=1-cos(alpha)/ sin(alpha)

These formulas can be used for all of the problems throughout section 10-3.

Ex.1: Simplify:

2sin(60)cos(60)

sin2(60)=sin(120)

Ex.2: Simplify:

1-cos(20)/ sin(20)

tan(20)/2=tan(10)

Ex.3: Simplify:

2cos^2(20)-1

cos2(20)= cos40

=4 square root of 5

These are 3 examples that will be used throughout section 10-3.

Hope you had a great weekend, because I sure did. :)

10-3 Double-Angle and Half-Angle

Double-angle Formulas:

Sin2α = 2sinαcosα cos2α = cos^2α-sin^2α cos2α = 2cos^2α-1 cos2α = 1-2sin^2α

Half-angle Formulas:

Tan2α = +/- 2tanα/1-tan^2α sinα/2 = +/- sqrt1-cosα/2 cosα/2 = +/- sqrt1+cosα/2

Tanα/2 = +/- sqrt1-cosα/1+cosα tanα/2 = sinα/1+cosα , 1-cosα/sinα

Ex. If sinα = 4/5 and 0<α

Sin2α =2sinαcosα

Already have sin so replace it – sin2α = 2(4/5)cosα

To find cosα just draw the unit circle and find out which quadrant it’s in with 0<α

Draw a triangle with that and it’s a 3, 4, 5 triangle. Cosα= 3/5

Sin2α = 2(4/5)(3/5) = 24/25

Cos2α = 1-2sin^2α = 1-2(4/5)^2 = -7/25

Go back to your triangle and find out that tanα = 4/3

Tan2α = 2tanα/1-tan^2α = 2(4/3)/1-(4/3)^2 = 8/3/-7/9 = -72/21

Double- and Half-Angle Formulas

Here they are:

sin2(theta)=2sin(theta)cos(theta)

cos2(theta)=cos^2(theta)-sin^2(theta)

cos2(theta)=1-2sin^2(theta)

cos2(theta)=2cos^2(theta)-1

tan2(theta)=2tan(theta)/1-tan^2(theta)

sin theta/2=+/-square root of 1-cos(theta)/2

cos theta/2=+/-square root of 1+cos(theta)/2

tan theta/2=+/-square root of 1-cos(theta)/1+cos(theta)

tan theta/2=sin(theta)/1+cos(theta)

tan theta/2=1-cos(theta)/sin(theta)

Example:

___________________________________________________________

Simplify.

cos^2(pi/12) - sin^2(pi/12)

=cos2(pi/12)

=cos2(15)

=cos30 degrees

=sqrt of 3/2

Sum and Difference

Sum and Difference Formulas for Sine and Cosine 

                Cos(α+β)=cosαcosβ-sinαsinβ

                Cos(α-β)=cosαcosβ+sinαsinβ

                Sin(α+β)=sinαcosβ+cosαsinβ

                Sin(α-β)=sinαcosβ-cosαsinβ

To set up sum and differences, we can use special values of 30˚, 60˚, and 45˚

1)       Find the exact value of cos 15˚

Cos15˚=cos(45˚-30˚)                               Replace 15 with 45-30

=cos45cos30+sin45sin30                       plug values into the formula

=(√2/2)(√3/2)+(√2/2)(1/2)                     replace special values√

=(√6/4)+(√2/4)                                         Simplify

=(√6+√2)/4

2)      Find exact value of cos 75˚

Cos75=cos(45+30)                                  Replace 15  with 45+30

=cos45cos30-sin45sin30                       plug values into the formula

=(√2/2)(√3/2)-(√2/2)(1/2)                     replace special values

=(√6/4)-(√2/4)                                         Simplify

=(√6-√2)/4

3)      Find exact value of sin 75˚

Sin75=sin(45+30)                                    Replace 75 with 45+30

=sin45cos30+cos45sin30                       plug values into the formula

=(√2/2)(√3/2)+(√2/2)(1/2)                     replace special values

=(√6/4)+(√2/4)                                         Simplify

=(√6+√2)/4

Jenna Roussel

10-3!

Double-Angle Formulas:

~sin2(alpha)=2sin(alpha)cos(alpha)

~cos2(alpha)=cos^2(alpha)-sin^2(alpha)

~cos2(alpha)=1-sin^2(alpha)

~cos2(alpha)=2cos^2(alpha)-1

~tan2(alpha)=2tan(alpha)/1-tan^2(alpha)

Half-Angle Formulas:

~sin(alpha)/2=+/-sqrt. of 1-cos(theta)/2

~cos(alpha)/2=+/-sqrt. of 1+cos(alpha)/2

~tan(alpha)/2=+/-sqrt. of 1-cos(alpha)/1+cos(alpha)

~tan(alpha)/2=sin(alpha)/ 1+cos(alpha)

~tan(alpha)/2=1-cos(alpha)/ sin(alpha)

You will use the formulas for all problems in section 10-3.

__________________________________________________

Ex.1: Simplify:

~2sin(40)cos(40)

sin2(40)= sin80

Ex.2: Simplify:

~1-cos(10)/ sin(10)

tan(10)/2= tan5

Ex.3: SImplify:

~2cos^2(15)-1

cos2(15)= cos30

=sqrt. of 3/2