Plane Curves

Plane Curves... yeah.

So the different types of curves we need to know are:

1. Lemniscate
2. Cardioid
3. Rose
4. Limascon of Pascal
5. Spiral of Archimedes

For the test, you will need to know what each one looks like, and how the equation of each one looks like.

A Lemniscate looks like:
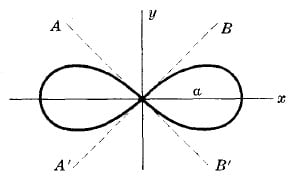and it's equation will either look like...

1. r² = a²cos2Θ
2. r = ± √(a²cos2Θ)
Ex. r² = 9cos2Θ
r = ± √(9cos2Θ)

A Cardioid resembles..a heart..kinda.
It's equation will look like ---> r = a + acosΘ.
Ex. r = 3 + 3cosΘ
r = 5 + 5cosΘ

A rose will obviously look like a flower of sorts.
The equation will look like: r = asinbΘ or r = acosbΘ

To find the number of petals, if b is odd, it has b petals. If b is even, it has 2b petals.

Ex. 3sin8Θ has 16 petals

3cos9Θ has 9 petals

A Limascon of Pascal looks similar to a Cardioid:
the equations looks like: r = b + acosΘ
the difference between a Cardioid and a Limascon is that b is not equal to a.

To find if it has an inner loop or not, if a is greater than b, it does, if a is less than b, it does not.

Ex. 3 + 5cosΘ does have an inner loop

5 + 3 cosΘ does not have an inner loop


A Spiral of Archimedes is a spiral, obviously :P
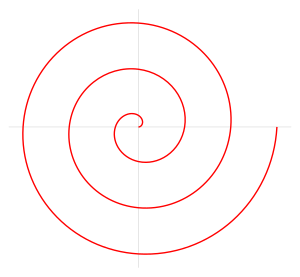LOOK HOW PRETTY!! Haha, uh, the equation is pretty much r = aΘ

Ex. r = 8Θ