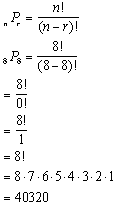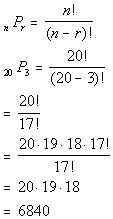DOMAIN AND RANGE
Domain-the interval of x values where the graph exists.
-Range-the interval of y values where the graph exists.
-Zeros x-int root-set=0 solve for x.
-To be a function the graph must pass the vertical line test.
-If given points the domain is the list of all x-values and the range is the list of all y-values in { }.
To find the Domain and Range you..
1. polynomials: domain (-infinity, infinity) always range (-infinity, infinity) odd always
2. square root: y=square root of x+/-number +/-a
To find domain of square root:
1. set inside the root=0 and solve
2. set up intervals
3. plug in, if you get a negative x is the interval
4. write answers in interval notation-use [ by the number range [a,infinity)
square root: y=square root of number - x^2 +/-a
To find domain:
1. set inside =0 solve
2. put answers in [-, ]
range: [0,square root of number] if a=0.
[0+a,square root of number+a] if a is positive
[0-a,square root of number-a] if a is negative
fraction:
To find domain:
1. factor top and bottom
2. cancel if possible and mark the number canceled
3. set bottom =0 and solve for x-values
4. write in interval notation stopping at number's found in 2 and 3
absolute value: domain: (-infinity,infinity)
range: [0+a,infinity) if opens up and a is positive
[0-a,infinity) if opens up and a is negative
(-infinity,0-a] if opens down and a is negative
(-infinity,0+a] if opens down and a is positive
Example 1:
Find the domain and range and tell whether each is a function.
g(t)= t+2/t^2+5t+8
1. t+2/(t+4)(t+2)
2. the (t+2)'s cancel x=-2
3. t+4=0 t=-4
4. (-infinity,-4) u (-4,-2) u (-2,infinity)